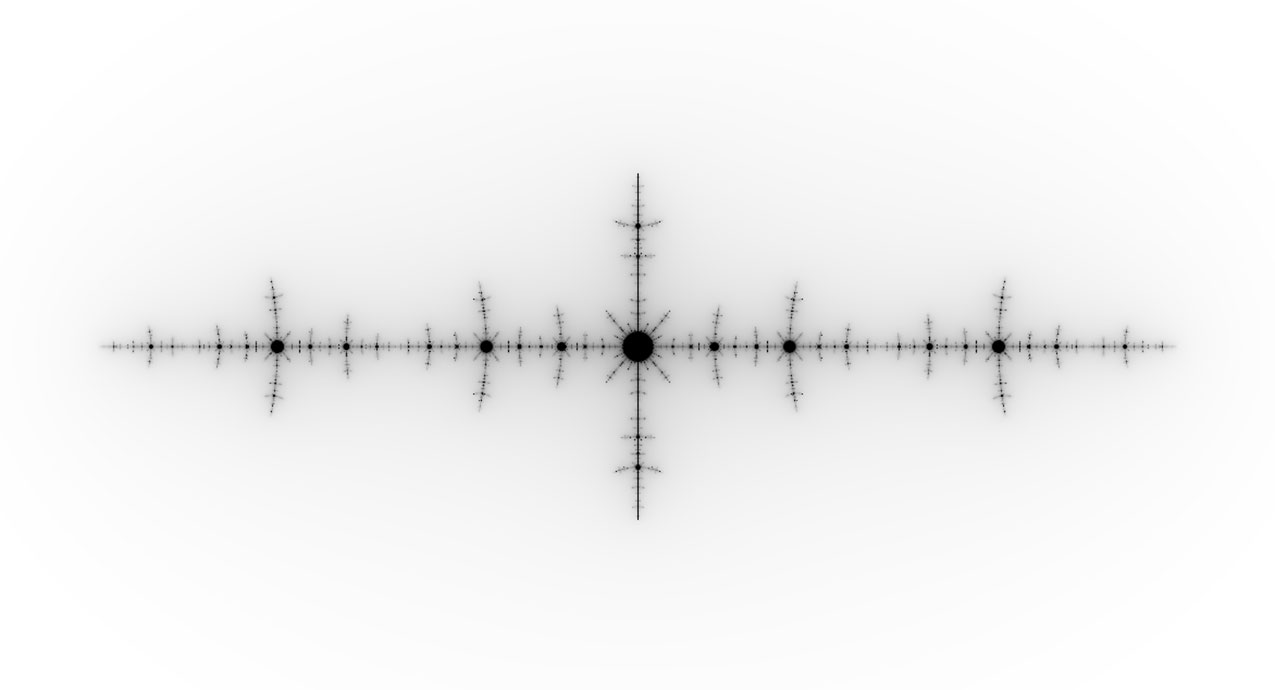
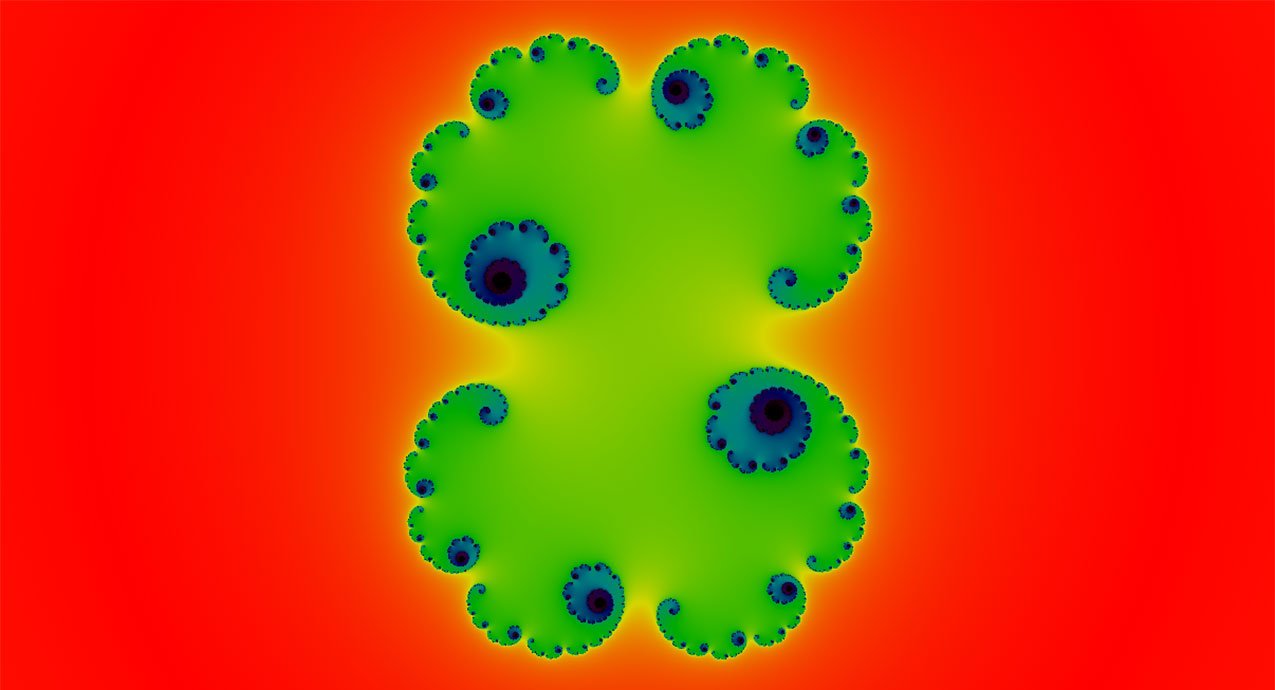
A funny story about me is how I got into web development. It essentially boiled down to me learning, and then becoming obsessed with, making programs on my TI-83 Plus calculator in a BASIC-like language designed just for the calculator. This made it a perfect portable IDE for someone learning how to program. I made minesweeper, lights out, D-Star (with custom level editor, I might add), and a program to view fractals! Well, apparently I forgot to upload that last one. And so began my obsession as an adult to relearn and recreate this with my new fancy web development skills I’ve picked up in the last 15 years. So basically, I did it in Javascript.
After some quick digging, I realized I was way smarter as a high schooler than I am now. How did I do this before? Complex numbers, complex plane, how to iterate correctly and determine if it has escaped toward infinity. And after I figured all that stuff out, I had to tackle more problems, how to zoom in, how to colorize (both grayscale and color as the calculator had neither). This was going to be a tough task.
(Also I’d like to point out all images in this post link to the fractal viewer itself, to see that image live)
No Framework
I wanted to not use a framework, as I did not see the need. This was a single page, single page application. 99% of the work would be done drawing to the canvas, and none of the inputs were related or reliant on any other elements. But, I did take a reactive approach, and it was cool to implement my own stateful app that has a setState function and batch renders state changes asynchronously. This part was definitely a little tricky but fun to work on.
There’s No i in Javascript
There’s no I in team and the same is true for Javascript. No I’m not talking about that “i” because I see it there after the r and before the p. I’m talking about imaginary numbers. When I made this on my graphing calculator, of course there is i, and I used it. It made calculating the equation easy. But with javascript it became a bit more difficult. Luckily, math in general tends to have lots of shortcuts, and that was also the case here. Here’s the magic for calculating Znew = Zold2 + C where both Zs and C are complex numbers:
const ZNewReal = Math.pow(ZOldReal, 2) - Math.pow(ZOldImaginary, 2) + Cr;
const ZNewImaginary = 2 * ZOldReal * ZOldImaginary + CImaginary;
const absoluteValue = Math.sqrt(Math.pow(ZNewReal, 2) + Math.pow(ZNewImaginary, 2));With the absense of i also comes an alternative way of dealing with complex numbers. We must refer to both the real and imaginary parts separately (where a complex number is written x + yi, x being the real part and i being the imaginary part).
Zooming In
Zooming in was not, in and of itself, that difficult. When the user clicks and drags a box to zoom in on, just save the left, right, top and bottom boundaries and that’s that…right? Well, as soon as you open that link in a window with a different aspect ratio, it gets all mucked up. Instead of saving the “viewport window”, I needed to save the origin (middle coordinate of the screen), and the delta of values between the x plane (real numbers) and y plane (imaginary numbers). This way I could render and view, at any zoom level, on any device and it will be centered and look correct.
Smoothing Color
When rendering, I would get pretty noticable lines where values would change abruptly. While this was mathematically correct, I’ve seen many more examples on the internet that looks much smoother. Since I am a very visual person (why I love working on the front end, and hey, I even have a BFA), this smoother kind of look is what I wanted to go for. A pretty clever way to smooth color, I found here. That was way easier than I thought it would be!
const newNumberOfIterations = actualNumberOfIterations - Math.log2(Math.log2(finalAbsoluteValueOfLastIterationResult));Sweet variable names, no?
The End
All in all, this was a lot of fun to work on and hope others enjoy it at least a fraction as much as I did. Check it out here, or just look at my screenshots below to see what all this talk is about (remember they are clickable!).